












































































 Algorytmy
Algorytmy
 Sortowanie tablic
Sortowanie tablic
program demonstracyjny sort_demo.zip (219kB)
Sortowanie polega na ustawieniu elementów zbioru w kolejności rosnącej lub
malejącej według pewnego kryterium (np. wartość liczbowa czy kolejność
alfabetyczna tekstów). Z punktu widzenia techniki komputerowej rozróżnia się
dwie grupy metod:
1. sortowanie tablic, czyli wszystkie dane są w każdej chwili dostępne (in
situ)
2. sortowanie plików, czyli dane są dostępne sekwencyjnie
Sortowanie tablic jest łatwiejsze i w literaturze można spotkac opis wielu metod
różniących się szybkością i złożonością algorytmu. Sortowanie plików jest sprawą
bardziej złożoną i z reguły wymaga tworzenia dodatkowych plików pomocniczych.
Poniżej opisane są najważniejsze metody sortowania.
Założenie: w procedurach dotyczących sortowania tablic zakładam następujące deklaracje:
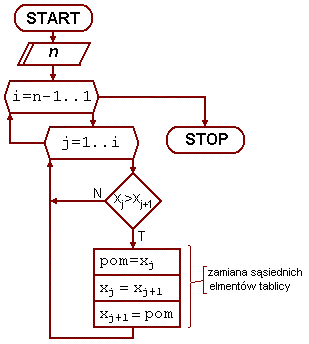
Polega na przeglądaniu tablicy i porównywaniu par sąsiednich elementów. Jeżeli ich porządek nie jest właściwy, to są zamieniane miejscami. Po jednym przejrzeniu tablicy ostatni jej element jest już na właściwym miejscu, dlatego można go pominąć w następnym przebiegu.
|
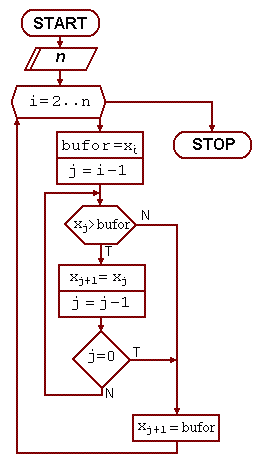
Metoda polega na przesiewaniu kolejnych elementów w kierunku początku tablicy
aż do znalezienia właściwego miejsca. W czasie sortowania początkowa część
tablicy jest już uporządkowana. Na początku zakłada się, że pierwszy element
jest na właściwym miejscu. Następny element porównuje się z poprzednim i w razie
potrzeby przesuwa się go w tył aż się znajdzie na swoim miejscu.
Metoda jest znana wszystkim karciarzom, gdyż właśnie w ten sposób zwykle
porządkują karty w ręku.
|
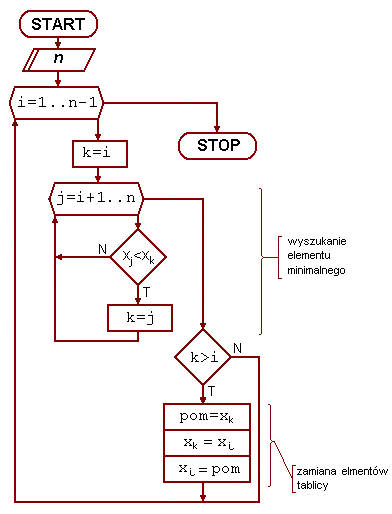
W czasie sortowania początkowa część tablicy jest już uporządkowana. Na
początku część uporządkowana jest pusta. Metoda polega na wyszukiwaniu w części
nieuporząkowanej elementu najmniejszego, a następnie zamianie go z pierwszym
elementem części nieuporządkowanej (staje się ostatnim elementem części
uporządkowanej).
Metoda ta wymaga bardzo dużej liczby porównań elementów.
|
Jest to zmodyfikowana metoda wstawiania. Można zauważyć, że przy wstawianiu elementu o małej wartości musi on "ominąć" dużą liczbę większych elementów. Wynika to stąd, że porównujemy i przestawiamy sąsiednie elementy. W metodzie Shella początkowo porównuje się elementy oddalone np. o połowę rozmiaru tablicy. W wyniku pierwszego przebiegu tablica jest już posortowana "co n/2". W drugim przebiegu sortujemy co n/4 rozmiaru, potem n/8, itd. Ostatni przebieg jest już zwykłym wstawianiem "co 1", ale z powodu znacznego uporządkowania tablicy element jest przesiewany na niewielką odległość.
Tak opisany sposób realizuje ciąg odległości (czytany od końca):
1 2 4 8 16 ...2*k
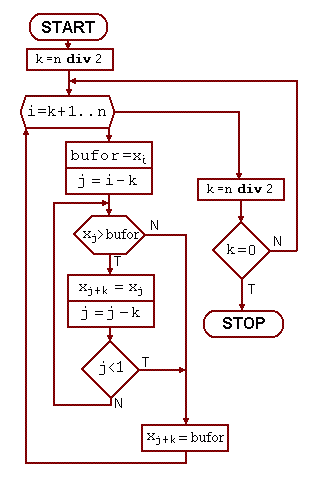 |
W wyniku analizy metody okazało się, że lepsze wyniki dają inne ciągi odległości. Najlepiej, gdy wyrazy ciągu nie są swoimi dzielnikami, np:
1 3 7 15 ... 2*k+1 1 2 5 14 ... 3*k-1 1 4 13 40 ... 3*k+1do góry
Metoda wykorzystuje strukturę zwaną stogiem (stosowane są również nazwy sterta i kopiec). Jest to drzewo binarne o kształcie jak na rysunku: Cechą wyróżniającą stóg jest jego uporządkowanie: Stóg można bardzo łatwo reprezentować w zwykłej tablicy czytając je kolejnymi rzędami. Odpowiada to następującym regułom: tab[1] - wierzchołek stogu tab[2*n] - lewy potomek węzła n tab[2*n+1] - prawy potomek węzła n |
Istotną procedurą pomocniczą jest przesianie. Jej celem jest przywrócenie właściwości stogu po zmianie wartości jego wierzchołka. Jest ona wykorzystywana w etapie tworzenia stogu oraz w etapie sortowania.
Algorytm sortowania:
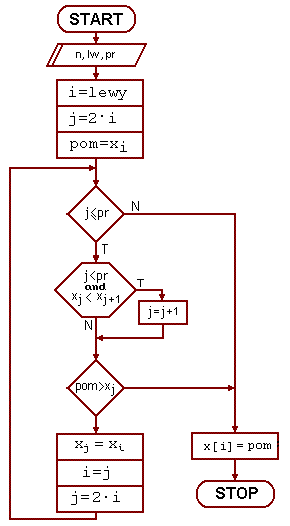
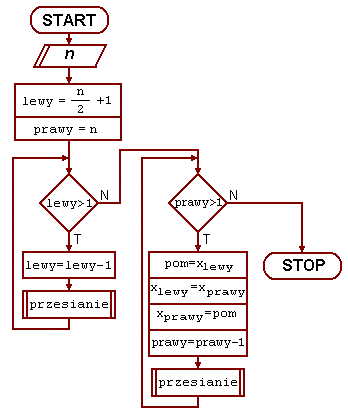 |
Jest to metoda, która w typowych przypadkach działa bardzo szybko (stąd nazwa). Odkrył ją w latach 60-tych XXw profesor Tony Hoare. Procedura wywoływana jest z dwoma parametrami określającymi indeksy pierwszego i ostatniego elementu.
Najpierw wybierany jest tzw. element osiowy, którym może być dowolny z
elementów tablicy (np pierwszy lub środkowy). Następnie tablica jest dzielona na
dwie części. W lewej są elementy mniejsze od osiowego, w prawej większe.
Poniższe procedury prezentują dwa sposoby podziału. Różnią się one złożonością
obliczeniową. Pierwszy charakteryzuje się mniejszą liczbą operacji podstawienia,
drugi mniejszą liczbą operacji porównania.
Następnie rekurencyjnie sortuje się obydwie części, o ile ich rozmiary są
większe od 1.
I JUŻ!
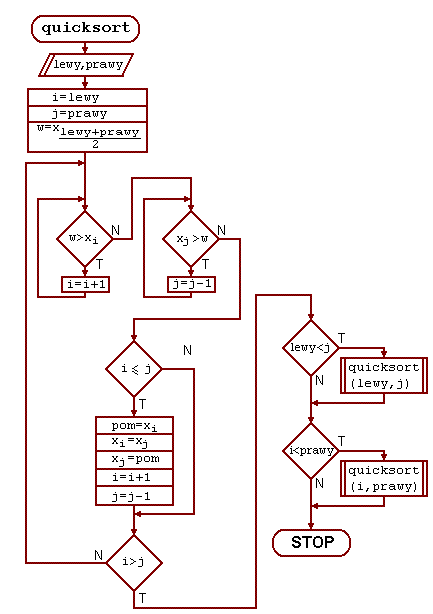 |
Metoda ta jest adaptacją dla tablic metody stosowanej do sortowania plików. Jest metodą rekurencyjną z gatunku "dziel i zwyciężaj".
Procedura sortująca otrzymuje dwa parametry oznaczające początek i koniec sortowanego ciągu (fragmentu tablicy):
Algorytm jest prosty:
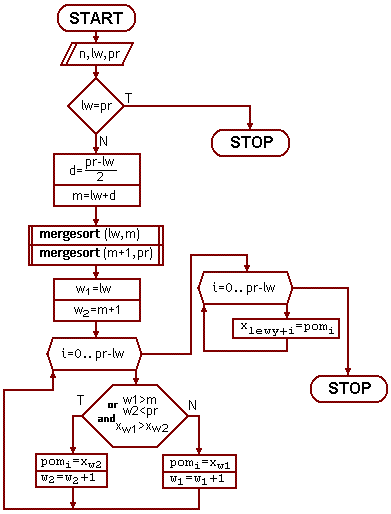 |



 © mgr inż. Piotr Kotarski, Kalety
© mgr inż. Piotr Kotarski, Kalety



