












































































 Algorytmy
Algorytmy
 Algorytmy klasyczne
Algorytmy klasyczne
program demonstracyjny euklides.zip (217kB)
Jest to jeden z najstarszych, znanych od starożytności algorytmów. Został on
opisany w wydanym przez Euklidesa 13-tomowym podręczniku do matematyki p.t.
"Elementy" ok 300pne. Algorytm dotyczy znalezienia największego
wspólnego dzielnika dwóch liczb całkowitych. W oryginale wyglądało to tak:
a) masz dwie liczby a i b, przy czym a>b,
b) dopóki a≥b wykonuj działanie a:=a-b,
c) jeżeli a<b i a≠0 to zamień miejscami a i b,
i wróć do punktu b),
d) jeżeli a=0 to wynikiem jest aktualna wartość b.
W praktycznej realizacji odejmowanie zastępujemy resztą z dzielenia (operacja "modulo"), nie trzeba również wstępnie porządkować zmiennych, gdyż w pierwszym przebiegu pętli i tak to nastąpi.
do góryprogram demonstracyjny pierwsze.zip (262kB)
Jest to algorytm również znany od starożytności. Dotyczy znalezienia liczb pierwszych w pewnym, ograniczonym zakresie liczb. Zasada jest następująca:
program demonstracyjny pierwsze.zip (262kB)
Rozkład liczby x na czynniki pierwsze polega na sprawdzaniu
podzielności tej liczby przez kolejne liczby piewsze k. Ponieważ
program "nie zna" liczb pierwszych sprawdzamy podzielność dla ciągu
liczb k = 2, 3, 5, 7, 9, ... (dalej kolejne nieparzyste).
Jeżeli liczba x jest podzielna przez k to:
a) k zapisujemy na liście czynników,
b) x modyfikujemy: x:=x div k,
c) powtarzamy sprawdzenie podzielności x przez k.
Proces można zakończyć, gdy k*k>x, gdyż takie wartości na pewno nie
będą czynnikami liczby x.
Jeżeli w wyniku poprzednich obliczeń wartość x>1, to jest ona
ostatnim czynnikiem.
Procedura Rozklad otrzymuje dwa parametry:
x - dana liczba,
i - ilość czynników.
Czynniki zapisywane są do tablicy.
Oczywiście, można wyniki wyprowadzać inaczej, np. na ekran lub do pliku. Nie zmienia to istoty algorytmu.
do góryJest to przykład eleganckiego i bardzo efektywnego algorytmu iteracyjnego. Służy do obliczenia pierwiastka kwadratowego (lub innego) z liczby rzeczywistej. Polega na znajdowaniu kolenych przybliżeń pierwiaska na podstawie poprzednich przybliżeń.
Załóżmy, że
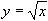
Wzór ten jest słuszny dla kwadratu o boku y i polu x. Problem więc polega na znalezieniu boku kwadratu o polu x.
Załóżmy, że mamy prostokąt o jednym boku równym 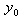 (dowolna, dodatnia liczba). Aby jego pole było równe x, to drugi bok musi być równy
(dowolna, dodatnia liczba). Aby jego pole było równe x, to drugi bok musi być równy 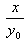 .
.
Oczywiste jest, że 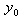 jest pierwiastkiem, jeżeli te boki są równe. W ogólnym przypadku tak nie jest, więc musimy obliczyć kolejne przybliżenie. Wyznaczamy je jako średnią arytmetyczną boków prostokąta. Tak otrzymujemy znany wzór iteracyjny:
jest pierwiastkiem, jeżeli te boki są równe. W ogólnym przypadku tak nie jest, więc musimy obliczyć kolejne przybliżenie. Wyznaczamy je jako średnią arytmetyczną boków prostokąta. Tak otrzymujemy znany wzór iteracyjny:
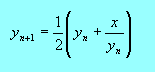
Pierwsze przybliżenie może być dowolne, np równe x.
Przykładowo dla y0=x=100:
0 100,0000000000000 1 50,5000000000000 2 26,2400990099010 3 15,0255301199868 4 10,8404346730269 5 10,0325785109606 6 10,0000528956427 7 10,0000000001399 8 10,0000000000000
Na przykładzie widać dużą zbieżność iteracji, co jest główną zaletą tego algorytmu. Po znalezieniu pierwszych poprawnych cyfr, ich ilość podwaja się w każej iteracji.
W praktycznych realizacjach algorytmu N-R w systemach cyfrowych (komputery, kalkulatory) pierwsze przybliżenie wyznacza się korzystająć z wewnętrznej, dwójkowej, zmiennoprzecinkowej reprezentacji liczby. Najprościej jest podzielić cechę liczby przez 2, np:
x = 1,5625 * 26 = 100
y0 = 1,5625 * 23 = 12,5
Jak widać niżej, rozwiązanie jest znacznie szybsze!
0 12,5000000000000 1 10,2500000000000 2 10,0030487804878 3 10,0000004646115 4 10,0000000000000
Algorytm N-R można uogólnić na pierwiastki wyższych stopni, stosując następujące wzory iteracyjne:
pierwiastek sześcienny: 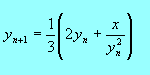
pierwiastek k-tego stopnia: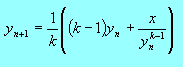



 © mgr inż. Piotr Kotarski, Kalety
© mgr inż. Piotr Kotarski, Kalety



